Научные статьи

Симметрия — наиболее простая категория, вследствие этого — наиболее общая. Она является кирпичиком (первоэлементом (ПЭ)) для определения других категорий: изо-полиморфизм (симметрия и изо-полиморфизм тесно взаимосвязаны между собой как отношения единства (R) и основания деления (А), конвергенция и дивергенция (симметризация и асимметризация), изомерия и неизомерия, омонимичность и неомонимичность, рефлексивность и антирефлексивность (симметричность самому себе).

Симметрией в рамках Общей теории систем Ю. А. Урманцева называется системная категория, обозначающая совпадение по признакам П систем С после изменений И. Иными словами, симметрия рассматривается как одна из реализаций абстрактной системы, чаще всего такого объекта-системы (ОS), в качестве первоэлементов которого выступают система С (определенная система как носитель симметрии) и признаки П (инварианты), в качестве отношений единства — отношение принадлежности признаков П системе С, а в качестве законов композиции — требование принадлежности этих признаков системе до и после изменений И (преобразований симметрии) [1, 192].

При других признаках П или изменениях И те же самые системы С могут оказаться несовпадающими частично (диссимметричными) или полностью (асимметричными). Таким образом, в рамках ОТСУ асимметрия — системная категория, обозначающая несовпадение по признакам П систем С после изменений И. Видим, категория симметрии дополнена ее противоположностью — асимметрией, с необходимостью ею предполагаемой и дополняющей ее до гармоничной пары симметрия-асимметрия. Иначе, любое нарушение симметрии компенсируется другим видом симметрии.

Упрощенно можем говорить, что симметрия — совпадение любых двух и т. д. объектов по любому основанию (релятивистское толкование). Уточнение оснований и дает нам наличие других, более конкретных категорий.

При этом основной закон композиции предполагает противоположность единице (в двоичной системе счисления) нуля, противоположность существованию отсутствие существования. Так, в данном случае, имея совпадение (симметрию), мы предполагаем наличие в качестве необходимого дополнения и противоположности соответствующее несовпадение (асимметрию). Таким образом, используя два признака С и А, мы имеем систему, состоящую из четырех подсистем.

Подсистема 4 (- -) — это универсум до всякой его классификации или до его классификации по признакам С и А.

Подсистемы 2 и 3 (соответственно + - и - +) представляют симметрию и асимметрию как таковые. Можем говорить, что почти невозможно найти полностью симметричные или полностью асимметричные объекты, то есть совпадающие относительно вообще всех (даже несущественных) признаков (можем привести в пример правые и левые объекты, изменение объектов во времени и т. д.). Поэтому чаще симметрия или асимметрия выявляются при исследовании одного или нескольких специально оговоренных (значимых, основных или случайных) признаков. В этих же подсистемах также находятся объекты, соответственно тождественные или нетождественные самому себе (рефлексивные или антирефлексивные).

Итак, симметрия и асимметрия — это предельные категории, показывающие совпадение-несовпадение по всем признакам, это 100% и 0% симметрии. Однако если основание деления не оговорено, сложно найти полностью симметричный или полностью асимметричный объект. Поэтому второй по наполняемости, вслед за подсистемой 4, будет подсистема 1 (+ +), где находятся системы, имеющие частичное совпадение при частичном несовпадении (диссимметрия).

Система симметрии-асимметрии непротиворечива, ибо, точно указав основания деления, сравнивая объекты, мы не выйдем за рамки нашего плюс-минусового кода. Эта система целостна, ибо охватывает абсолютно все объекты универсума. Так, любой объект, который, мы еще не начали сравнивать, находится в подсистеме 4. Приложив к таким объектам основание и проведя сравнение, мы сами переведем такую пару в подсистемы 3 или 2. Далее, находя новые основания и проводя по ним сравнения, может появиться возможность перехода объектов из подсистем 3 или 2 в подсистему 1. Таким образом, мы можем констатировать пять теоретически возможных путей развития, или построить систему изменений (Таблица 1):

Таблица 1

При изучении системы изменений основными задачами будут выделение симметрии на разных уровнях, в разных системах, определение групп симметрии на основе преобразований симметрии по определенным признакам, определение группового характера изменений симметрии единиц уровнем ниже (попытка представить любую систему изменяющейся по определенным правилам, подчиняющимся симметрии (симметрия развития), прогноз развития.

Чаще всего нам не надо характеризовать объекты через все их признаки. Сопоставление объектов показывает, что с точки зрения сходств/различий (совпадений/несовпадений) они могут характеризоваться по множеству признаков по отдельности или в сумме отдельных признаков, составляющих каждый объект-систему. Число признаков должно быть необходимым и достаточным, а также отметим, что обязательно наличие хотя бы одного признака (напомним, что симметрия — совпадение систем по признакам после изменений). Число теоретически возможных вариантов (результатов) при том или ином количестве признаков всегда известно и определено числом 2n, где n — количество признаков. Так, 1 признак дает 2 варианта, 2 признака — 4 варианта, 3 признака — 8, 4 — 16 и т. д. Каждый раз необходимая точность результата определяет количество признаков (при необходимости большей детализации большим будет и количество признаков), однако наиболее удобным при сравнении представляется использование 2 или 3 признаков. При большем количестве признаков их число может быть сведено к 2 или 3, но эти признаки должны быть наиболее общими и значимыми для данной системы объектов.

Самыми общими можно признать количество, качество, отношение. Так, советский биолог и философ академик Ю. А. Урманцев, выводя основной закон своей Общей теории систем, указал, что возможны лишь четыре основных вида преобразований объекта: тождественное, количественное, качественное, относительное. Это преобразование в себя (дление объекта во времени), количества, качества, отношения [2, 53].

Для примера рассмотрим изменения количества.

Закон количественного преобразования говорит, что «в подсистеме М... имеет место либо прибавление (П), либо вычитание (В), либо прибавление и вычитание „первичных элементов“» [2, 63]. Присвоив (+) значение наличия изменения, а знаку (-) — отсутствия изменений, составим непротиворечивую целостную систему преобразований в виде плюс-минусового куба (Рис. 1). Под прибавлением мы понимаем увеличение количества букв в слове, под вычитанием — уменьшение их количества. Возможен учет не только букв, но и звуков, фонем, их комбинаторики, количества слогов или морфем; изменений иного рода. Для целей данной статьи таковым явлением будет омонимия, но при изучении количественных характеристик любого лингвистического явления указанный ниже порядок будет релевантен, и будет приводить к получению сходных и легко сравнимых друг с другом результатов.

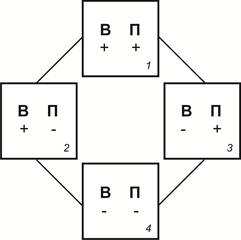
Рис. 1

Подсистема 4 соответствует неизменности объекта во времени. Эта подсистема обязательна в нашей классификации для ее полноты, ибо находим пары омонимов, которые длятся во времени без количественных изменений (меццо — меццо). Значит, в подсистеме 4 находятся неизменяемые слова, а в подсистемах 3 (чистое прибавление) и 2 (чистое вычитание) наличие изменения обязательно.

Подсистема 1 характеризует изменение пары объектов-систем обязательным и вычитанием, и прибавлением.

Представим подсистему 1 предыдущей системы четырьмя новыми подсистемами, которые точнее характеризуют преобразование, осуществляемое обязательным прибавлением и вычитанием. Учитывая, это, основным будем считать признак наличия/отсутствия прибавления и вычитания в обоих объектах-системах. Примем за (2) вычитание или прибавление у обоих объектов, а за (1) — только у одного объекта.

Подсистема 22 — изменения с обязательными вычитанием и прибавлением в обоих объектах-системах. Здесь находятся примеры всех типов омонимии: Поля — Поли и полоть — поли; лат. venio [‘приходить’] — ventum и ventus — ventum [‘ветер’]; rosa — rosis (dat. sg.) и rosa — rosis (abl. pl.); pilum [‘пестик’] — pili и pilum [‘дротик’] — pili.

Подсистема 21 — вычитание в двух омоисходах при прибавлении к одному: пить — пили и пилить — пили, pello [‘толкать’] — pelli и pellis [‘мех’] — pelli.

Подсистема 12 — вычитание в одном при прибавлении к обоим: ворон — вороном и вороной — вороном, vir [‘мужчина, муж’] — viri и virus [‘яд’] — viri. Здесь видим примеры только лексико-грамматической омонимии.

Подсистема 11 показывает, что вычитание и прибавление использованы каждое только в одном омоисходе: гол — голов и голова — голов.

Преобразования не всегда происходят одинаково: возможно вычитание-прибавление одинаковых элементов (брак — брака и брак — брака) или неодинаковых (полый — полого и пологий — полого). Всю возможную комбинаторику преобразований с помощью вычитания и прибавления в обоих элементах пары подсистемы 22 можно представить следующим образом (Рис. 2.): (Р) — вычитание или прибавление равных элементов; (Н) — неравных:

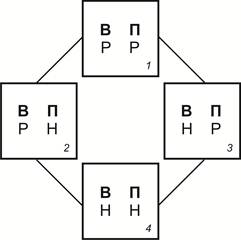
Рис. 2

В подсистеме 4 находим случаи вычитания и прибавления неодинаковых отрезков: класть — клади и кладь — клади, vinco [‘побеждать’] — victum и vivo [‘жить’] — victum. Видим, что вычитаться и прибавляться могут абсолютно разные (асимметричные) отрезки и частично разные (диссимметричные).

Подсистема 3 показывает, что могут вычитаться неодинаковые отрезки и прибавляться одинаковые: судить — сужу и сузить — сужу. Преобразование посредством одинаковых отрезков чаще всего указывает на парадигматическое изменение (словоизменение), а неодинаковые элементы позволяют связывать далекие друг от друга объекты — компенсировать дифференциальную разницу — (см. вывод о том, что асимметрия более информативна [3, 205]).

Это же касается подсистемы 2. К изменению отношения между объектами приводит асимметризация (действие с неравными элементами): pareo [‘являться’] — pares и paro [‘приготовлять’] — pares.

Подсистема 1 в этом отношении наиболее предсказуема. Сюда попадают лексические омонимы: paro [‘приготовлять’] — paras и paro [‘равнять’] — paras.

Обобщая классификации, которые мы составили выше, построим общую треугольную (т. к. порядок операций в омопаре не важен) декартову матрицу (Таблица 2). По вертикали покажем наличие/отсутствие вычитания (В) и/или прибавления (П) в первом элементе омопары, по горизонтали — во втором. Цифра показывает, в скольких элементах конкретное действие происходит:

Таблица 2

Приведем примеры заполнения матрицы.

1. Мести — мету и мета — мету, vivo [‘жить’] — victum и vinco [‘побеждать’] — victum. Здесь же находятся лексическая омонимия типа охота — охоте и охота — охоте и грамматическая омонимия типа мама — маме (dat. sg. и loc. sg.).

2. Валить — вали и Валя — Вали, pello [‘толкать’] — pelli и pellis [‘мех’] — pelli.

3. Вороной — вороном и ворон — вороном, paro [‘приготавливать’] — pares и pareo [‘являться’] — pares.

4. Такса — такс и такса — такс, parare — para и parare — para. Здесь находится и грамматическая омонимия типа мама — мам (gen. pl.) и мам (voc. sg.).

5. Кол — колок и кол — колок, ключ — ключа и ключ — ключа, parāre — parārem и parāre — parārem. И здесь есть грамматическая омонимия человек — человека (acc. sg.) и человека (gen.sg.).

6. Рука — рукой и рукой, sine [‘без’] и sino [‘изгибать’] — sine.

7. Череп — черепах и черепаха — черепах, as [‘монета’] — assi и assis [‘ось’] — assi.

8. Ворон — ворона и ворона, fide [‘верно’] и fides [‘доверие’] — fide.

9. Ворона — ворон и ворон, as — assis и assis — assis.

10. Но (междометие) и но (союз), pilum — pilum и pilum — pilum; paro и paro, а также грамматическая омонимия дворник ‘устройство’ как nom. и acc. sg.

Подобный порядок построения мы могли бы использовать для иных лингвистических явлений. Так, для получения изомеров мы можем прибавлять или отнимать одинаковые отрезки (пустить — ступить, пустил — ступил), или неодинаковые (рука — рукам, курица — курам)

Таким образом, мы показали систему количественных изменений на примере омонимии (напомним, что омонимизация — это процесс симметризации). Симметрия формы образуется в результате вычитания или прибавления либо букв, либо морфем, которыми различались две несимметричные до преобразования словоформы (дифференциальная разница). В рамках данной статьи мы не останавливались на вопросе, совпадают ли между собой морфемы данного конкретного языка и дифференциальные разницы, операции с которыми и приводят к выравниванию форм и проявлению того или иного лингвистического явления. Однако при утвердительном ответе на этот вопрос такой подход позволил бы упростить распознавание компьютером флексий, а возможно, и других аффиксов.

Литература

1. Урманцев, Ю. А. Симметрия и асимметрия как категории ОТС: их природа и соотношение / Ю. А. Урманцев // Система. Симметрия. Гармония. — Москва : Мысль, 1988. — С. 191–200.

2. Урманцев, Ю. А. Общая теория систем: состояние, приложения и перспективы развития / Ю. А. Урманцев // Система. Симметрия. Гармония. — Москва : Мысль, 1988. — С. 38–130.

3. Карпов, В. А. Язык как система / В. А. Карпов. — Минск : Вышэйшая школа, 1992. — 302 с.

Скачать статью (rar)Скачать статью (pdf)

Сведения об авторе (2009 г.): Гомон Дмитрий Николаевич — кандидат филологических наук, доцент кафедры классической филологии Белорусского государственного университета (Минск).

Выходные данные: Филологические штудии = Studia philologica : сб. науч. ст. / под ред. Г. И. Шевченко, К. А. Тананушко ; редкол.: А. В. Гарник [и  др.]. — Вып. 7. — Минск, 2009. — С. 13–19.

ISBN 978-985-518-201-7.